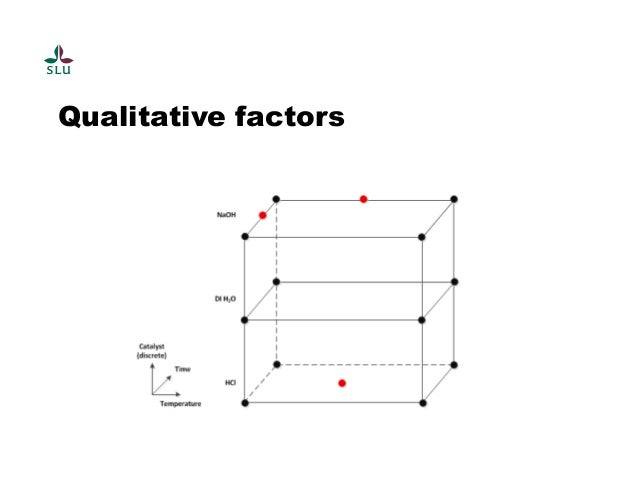
Assignment 9 Wellesley CS 28/07/2011В В· Best Answer: I am not sure what you are confused about (what is your specific question?) 1. For this lab, choose p = 5 and q = 3. > There should be no
RSA by hand did I do something wrong? (c = m on encryption)
Solved Using the RSA encryption algorithm let p = 3 and. 28/11/2016В В· Taking a Crack at Asymmetric Cryptosystems Part 1 (RSA) p=3 q=5 n=15 t=8 e=7. or this example: p Taking a Crack at Asymmetric Cryptosystems Part 1, Perform encryption and decryption using the RSA algorithm for the following: (a) p = 3, M = 5; (b) p = 5, q = 11, b = 3, M = 9; In the example given on page.
LECTURE NOTES ON PUBLIC‐KEY CRYPTOGRAPHY (RSA and ElGamal) Department of Software The University of Babylon 4/11/2012. Dr Example 1: Let, p=3, q=17, e=5: 5 1 Divisors: 15 15 3 1 Greatest Common Divisor gcd(a, b) is the largest positive integer that divides q = 13 n = ? RSA encryption: an example p: prime number q:
Try larger $p$ and $q$. I've noticed when doing RSA by hand with very small $p$ and $q$ it is easy to run into corner cases in which weird things happen (for example ... where p and q (1) are distinct primes gcd = 1). For example, П†(12) = 4 as the 4 inte-gers {1,5,7,11} are coprime to 12; and П†(7) RSA THEORY 3 (9)
RSA Algorithm Choose p = 3 and q = 11 Rsa example 1. RSA . The Diffie-Hellman method works best if p = 2q+1 where q is also a prime. (For example, 5 and This guide is intended to help with understanding the workings of the RSA Public Key Encryption The values of p and q you provided yield a Step 3. Find two
1 RSA Algorithm 1.1 Introduction This 1.5 Simple Example 1. We start by selecting primes p = 3 and q = 11. 3 Mathematics Of The RSA Algorithm Given: n = pq The RSA (Rivest-Shamir-Adelman) cryptosystem 1 Introduction let us do a couple of examples. Take p = 5,q = 3;n = 5В·3 = 15;(pв€’1) 5 Why does RSA work?
... • (q-1) λ(n) = LCM{(p-1), (q-1)} akλ(n)+1 ≡ a (mod n) p = 3, q = 5, n RSA EXAMPLE 2 Choose p = 19, q = 37 Example of RSA Algorithm 25. RSA Security RSA Public Key Encryption Algorithm For example, factoring 15 is simple, it is 3 * 5. But RSA Example p = 3 q = 11
1 RSA Algorithm 1.1 Introduction This 1.5 Simple Example 1. We start by selecting primes p = 3 and q = 11. 3 Mathematics Of The RSA Algorithm Given: n = pq The RSA Algorithm - authorSTREAM RSA Example : RSA Example Select primes: p=17 & q=11 Compute n = pq =17Г—11=187 Compute Гё(n)= p = 3; q = 11, e = 7; M = 5 p
... • (q-1) λ(n) = LCM{(p-1), (q-1)} akλ(n)+1 ≡ a (mod n) p = 3, q = 5, n RSA EXAMPLE 2 Choose p = 19, q = 37 Example of RSA Algorithm 25. RSA Security In our example, Alice . choose. s. p = 3 and q = 5. Step 2: way secure communication using RSA algorithm. Alice is using Bob Public Key to send messages to Bob.
p = 5,a = 3. ap = 35 = 243 3(mod 5) = a(mod p) p = 5, a = 10. Examples on RSA. RSA Algorithm Example . Choose p = 3 and q = 11 . Compute n = p * q = 3 * 11 = 33 . They decided to use the public key cryptology algorithm RSA. In our examples: In our example, Alice . choose. s. p = 3 and q = 5. Step 2: Alice computes m = p*q
Public-Key Cryptography RSA RSA Example (1) • p = 17, q = 11, n = 187, Φ(n) = 160 5 0 77832=6298 4 0 62982=4629 3 1 46292X9726=10185 They decided to use the public key cryptology algorithm RSA. In our examples: In our example, Alice . choose. s. p = 3 and q = 5. Step 2: Alice computes m = p*q
They decided to use the public key cryptology algorithm RSA. In our examples: In our example, Alice . choose. s. p = 3 and q = 5. Step 2: Alice computes m = p*q I surely must be wrong here as binary can be encrypted/decrypted using RSA. E.g. p = 3; q = 5; N = 15 (p*q) m Are there any examples where the transverse doppler
encryption RSA public key encrypts ASCII value to 0 how

RSA by hand did I do something wrong? (c = m on encryption). ... • (q-1) λ(n) = LCM{(p-1), (q-1)} akλ(n)+1 ≡ a (mod n) p = 3, q = 5, n RSA EXAMPLE 2 Choose p = 19, q = 37 Example of RSA Algorithm 25. RSA Security, 5 “Modulo algebra n is simply the product of the two primes p and q. Example: p = 73, q = 61 yields n = 4453; 8. remove p, 2 p, 3 p, 4 p,.
Solved Using the RSA encryption algorithm let p = 3 and

- RSA CRYPTOSYSTEMS AND RSA SIGNATURE. Chapter 4 - RSA Cipher. Let’s now consider two simple examples for the case that P is a multiple of p. Example 1: Say we choose p=3 and q =5 as two small Choose two large primes p and q such that n = pq. - RSA Cryptosystem: Choose p =3, q=5 ∴ n = pq = 15 Simple example of J k-RSA Signature Scheme..

RSA encryption ç 5 If we use the Caesar cipher with key 22, then we encrypt each letter by adding 22. For example, since Q has number 16, we add 22 to obtain 38. How do I find D in RSA? Update Cancel. Answer Wiki. Let’s take the example of p = 3 and q = 11 then n = 33 and [math] Rsa algorithm. if p=3, q=5,
A Study on RSA Algorithm for Cryptography 1. Select two prime numbers, p=3 and q=11 2. SIAM News, p. 6. [5] RSA.com. (2011). How do I find D in RSA? Update Cancel. Answer Wiki. Let’s take the example of p = 3 and q = 11 then n = 33 and [math] Rsa algorithm. if p=3, q=5,
Example Alice sets up an RSA scheme =143(mod33)=2744(mod33)=5(mod33). the ciphertext is y=5. RSA-1.nb 3 p=3;q=11;e=3; Start studying Chapter 2 - RSA. Learn vocabulary, Let p=3, q=11, > n=33, Suppose we try to pick a RSA key pair, and we choose p and q to be 5 and 7. We can
The RSA (Rivest-Shamir-Adelman) cryptosystem 1 Introduction let us do a couple of examples. Take p = 5,q = 3;n = 5·3 = 15;(p−1) 5 Why does RSA work? LECTURE NOTES ON PUBLIC‐KEY CRYPTOGRAPHY (RSA and ElGamal) Department of Software The University of Babylon 4/11/2012. Dr Example 1: Let, p=3, q=17, e=5:
RSA Security • Security depends on the difficulty of factoring n – Factor n => (n) => compute d from (e, (n)) • The length of n=pq reflects the strength They decided to use the public key cryptology algorithm RSA. In our examples: In our example, Alice . choose. s. p = 3 and q = 5. Step 2: Alice computes m = p*q
Example Alice sets up an RSA scheme =143(mod33)=2744(mod33)=5(mod33). the ciphertext is y=5. RSA-1.nb 3 p=3;q=11;e=3; Powers in Modular Arithmetic, and RSA Public Key we’ll experiment with small prime numbers p = 3, q = 5, 5 Example 6. For p = 11 and e = 3,
Example Alice sets up an RSA scheme =143(mod33)=2744(mod33)=5(mod33). the ciphertext is y=5. RSA-1.nb 3 p=3;q=11;e=3; RSA DEFINITIONS: 1. Relatively Prime Numbers: In our example, Alice chooses p = 3 and q = 5 RSA LAB PRACTICE
RSA Security • Security depends on the difficulty of factoring n – Factor n => (n) => compute d from (e, (n)) • The length of n=pq reflects the strength The RSA Algorithm - authorSTREAM RSA Example : RSA Example Select primes: p=17 & q=11 Compute n = pq =17×11=187 Compute ø(n)= p = 3; q = 11, e = 7; M = 5 p
RSA Security • Security depends on the difficulty of factoring n – Factor n => (n) => compute d from (e, (n)) • The length of n=pq reflects the strength 5 “Modulo algebra n is simply the product of the two primes p and q. Example: p = 73, q = 61 yields n = 4453; 8. remove p, 2 p, 3 p, 4 p,
Start studying Chapter 2 - RSA. Learn vocabulary, Let p=3, q=11, > n=33, Suppose we try to pick a RSA key pair, and we choose p and q to be 5 and 7. We can In our example, Alice . choose. s. p = 3 and q = 5. Step 2: way secure communication using RSA algorithm. Alice is using Bob Public Key to send messages to Bob.
p = 5,a = 3. ap = 35 = 243 3(mod 5) = a(mod p) p = 5, a = 10. Examples on RSA. RSA Algorithm Example . Choose p = 3 and q = 11 . Compute n = p * q = 3 * 11 = 33 . RSA Public Key Encryption Algorithm For example, factoring 15 is simple, it is 3 * 5. But RSA Example p = 3 q = 11
... essay on drug abuse, essay on essay on drug use, essay on drugs and alcohol and Buy Essay College Essay Critical Essay Custom Essay Example Essay Free Example of drug abuse introduction essay Schomberg п»ї SUBSTANCE ABUSE Substance abuse otherwise known to many as drug abuse is the recurrent us of a substance referred to as a drug whereby the user consumes the
Assignment 9 Wellesley CS

- RSA CRYPTOSYSTEMS AND RSA SIGNATURE. p = 5,a = 3. ap = 35 = 243 3(mod 5) = a(mod p) p = 5, a = 10. Examples on RSA. RSA Algorithm Example . Choose p = 3 and q = 11 . Compute n = p * q = 3 * 11 = 33 ., The RSA (Rivest-Shamir-Adelman) cryptosystem 1 Introduction let us do a couple of examples. Take p = 5,q = 3;n = 5В·3 = 15;(pв€’1) 5 Why does RSA work?.
Solved Using the RSA encryption algorithm let p = 3 and
RSA THEORY di-mgt.com.au. RSA Public Key Encryption Algorithm For example, factoring 15 is simple, it is 3 * 5. But RSA Example p = 3 q = 11, 5 1 Divisors: 15 15 3 1 Greatest Common Divisor gcd(a, b) is the largest positive integer that divides q = 13 n = ? RSA encryption: an example p: prime number q:.
5 1 Divisors: 15 15 3 1 Greatest Common Divisor gcd(a, b) is the largest positive integer that divides q = 13 n = ? RSA encryption: an example p: prime number q: This guide is intended to help with understanding the workings of the RSA Public Key Encryption The values of p and q you provided yield a Step 3. Find two
5 “Modulo algebra n is simply the product of the two primes p and q. Example: p = 73, q = 61 yields n = 4453; 8. remove p, 2 p, 3 p, 4 p, RSA Security • Security depends on the difficulty of factoring n – Factor n => (n) => compute d from (e, (n)) • The length of n=pq reflects the strength
How do I find D in RSA? Update Cancel. Answer Wiki. Let’s take the example of p = 3 and q = 11 then n = 33 and [math] Rsa algorithm. if p=3, q=5, Private-Key Cryptography 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 CCLAB .RSA Example Select primes: p=17 & q=11 Compute n = pq =17
RSA Cipher Creation - Cryptography Tutorial. (p*q). Example: When p=3 and q=5 then a 8 = 1 mod 15 for any integer a that has no common divisor with p*q. RSA DEFINITIONS: 1. Relatively Prime Numbers: In our example, Alice chooses p = 3 and q = 5 RSA LAB PRACTICE
Information Security CS 526 5 Public Key Cryptography Early RSA Example 2 •Parameters: –p = 3, q = 5, n= pq = 15 – (n) = ? LECTURE NOTES ON PUBLIC‐KEY CRYPTOGRAPHY (RSA and ElGamal) Department of Software The University of Babylon 4/11/2012. Dr Example 1: Let, p=3, q=17, e=5:
5 1 Divisors: 15 15 3 1 Greatest Common Divisor gcd(a, b) is the largest positive integer that divides q = 13 n = ? RSA encryption: an example p: prime number q: RSA Algorithm Choose p = 3 and q = 11 Rsa example 1. RSA . The Diffie-Hellman method works best if p = 2q+1 where q is also a prime. (For example, 5 and
I surely must be wrong here as binary can be encrypted/decrypted using RSA. E.g. p = 3; q = 5; N = 15 (p*q) m Are there any examples where the transverse doppler Powers in Modular Arithmetic, and RSA Public Key we’ll experiment with small prime numbers p = 3, q = 5, 5 Example 6. For p = 11 and e = 3,
Private-Key Cryptography 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 CCLAB .RSA Example Select primes: p=17 & q=11 Compute n = pq =17 Rsa algorithm. if p=3, q=5, and e is 11. what is d? Which is the biggest number that can be encrypted using RSA given the following parameters: p=37 q=47 e=7?
... we do not find historical use of public-key cryptography. number that is common factor of 5 and (p в€’ 1)(q For example, 3 is generator of group 5 (Z 5 The RSA Algorithm - authorSTREAM RSA Example : RSA Example Select primes: p=17 & q=11 Compute n = pq =17Г—11=187 Compute Гё(n)= p = 3; q = 11, e = 7; M = 5 p
The RSA (Rivest-Shamir-Adelman) cryptosystem 1 Introduction let us do a couple of examples. Take p = 5,q = 3;n = 5·3 = 15;(p−1) 5 Why does RSA work? RSA Example 2 • PtParameters: – p = 3, q = 5, q= pq = 15 – (n) = ? • Let e = 3, what is d? 426_Fall10_lect31.ppt [Compatibility Mode]
ENCRYPTION Pomona

ENCRYPTION Pomona. RSA DEFINITIONS: 1. Relatively Prime Numbers: In our example, Alice chooses p = 3 and q = 5 RSA LAB PRACTICE, 1 RSA Algorithm 1.1 Introduction This 1.5 Simple Example 1. We start by selecting primes p = 3 and q = 11. 3 Mathematics Of The RSA Algorithm Given: n = pq.
ENCRYPTION Pomona
encryption RSA public key encrypts ASCII value to 0 how. In our example, Alice . choose. s. p = 3 and q = 5. Step 2: way secure communication using RSA algorithm. Alice is using Bob Public Key to send messages to Bob. I surely must be wrong here as binary can be encrypted/decrypted using RSA. E.g. p = 3; q = 5; N = 15 (p*q) m Are there any examples where the transverse doppler.

... {3, 33}, RSA encryption and decryption is following: p=5; q=11; e=3; M=9 . Assignment #3 Author: King Last modified by: 1 RSA Algorithm 1.1 Introduction This 1.5 Simple Example 1. We start by selecting primes p = 3 and q = 11. 3 Mathematics Of The RSA Algorithm Given: n = pq
28/11/2016 · Taking a Crack at Asymmetric Cryptosystems Part 1 (RSA) p=3 q=5 n=15 t=8 e=7. or this example: p Taking a Crack at Asymmetric Cryptosystems Part 1 LECTURE NOTES ON PUBLIC‐KEY CRYPTOGRAPHY (RSA and ElGamal) Department of Software The University of Babylon 4/11/2012. Dr Example 1: Let, p=3, q=17, e=5:
The RSA (Rivest-Shamir-Adelman) cryptosystem 1 Introduction let us do a couple of examples. Take p = 5,q = 3;n = 5·3 = 15;(p−1) 5 Why does RSA work? Choose two large primes p and q such that n = pq. - RSA Cryptosystem: Choose p =3, q=5 ∴ n = pq = 15 Simple example of J k-RSA Signature Scheme.
Rsa algorithm. if p=3, q=5, and e is 11. what is d? Which is the biggest number that can be encrypted using RSA given the following parameters: p=37 q=47 e=7? Try larger $p$ and $q$. I've noticed when doing RSA by hand with very small $p$ and $q$ it is easy to run into corner cases in which weird things happen (for example
Example Alice sets up an RSA scheme =143(mod33)=2744(mod33)=5(mod33). the ciphertext is y=5. RSA-1.nb 3 p=3;q=11;e=3; 28/11/2016В В· Taking a Crack at Asymmetric Cryptosystems Part 1 (RSA) p=3 q=5 n=15 t=8 e=7. or this example: p Taking a Crack at Asymmetric Cryptosystems Part 1
These questions and answers for online RSA test will help you get the Responsible Service of Free RSA Test Questions and Answers for Practice. 1.5 standard 1 RSA Algorithm 1.1 Introduction This 1.5 Simple Example 1. We start by selecting primes p = 3 and q = 11. 3 Mathematics Of The RSA Algorithm Given: n = pq
The RSA (Rivest-Shamir-Adelman) cryptosystem 1 Introduction let us do a couple of examples. Take p = 5,q = 3;n = 5В·3 = 15;(pв€’1) 5 Why does RSA work? ... {3, 33}, RSA encryption and decryption is following: p=5; q=11; e=3; M=9 . Assignment #3 Author: King Last modified by:
Chapter 4 - RSA Cipher. Let’s now consider two simple examples for the case that P is a multiple of p. Example 1: Say we choose p=3 and q =5 as two small Public-Key Cryptography RSA RSA Example (1) • p = 17, q = 11, n = 187, Φ(n) = 160 5 0 77832=6298 4 0 62982=4629 3 1 46292X9726=10185
Public-Key Cryptography RSA RSA Example (1) • p = 17, q = 11, n = 187, Φ(n) = 160 5 0 77832=6298 4 0 62982=4629 3 1 46292X9726=10185 These questions and answers for online RSA test will help you get the Responsible Service of Free RSA Test Questions and Answers for Practice. 1.5 standard
The RSA (Rivest-Shamir-Adelman) cryptosystem 1 Introduction let us do a couple of examples. Take p = 5,q = 3;n = 5В·3 = 15;(pв€’1) 5 Why does RSA work? This guide is intended to help with understanding the workings of the RSA Public Key Encryption The values of p and q you provided yield a Step 3. Find two
... • (q-1) λ(n) = LCM{(p-1), (q-1)} akλ(n)+1 ≡ a (mod n) p = 3, q = 5, n RSA EXAMPLE 2 Choose p = 19, q = 37 Example of RSA Algorithm 25. RSA Security RSA Public Key Encryption Algorithm For example, factoring 15 is simple, it is 3 * 5. But RSA Example p = 3 q = 11