Lean Manufacturing concept work in progress (WIP) Work in progress (WIP) In a large manufacturing facility even small amounts of WIP can add up to a large sums of capital Examples and uses of work in progress
Value Stream Mapping for Lean Manufacturing Implementation
Manufacturing Manager Resume Samples JobHero. Scheduling dependent work cells 13 Example of an unbalanced configuration 15 Lean manufacturing Lean manufacturing: Capable to promise and kanban job, Continuous Flow Process Example. such as completing one-time work for a client. You can find free templates and make lean manufacturing diagrams with Lucidchart..
Lean Manufacturing Assessment Internal customers are the next work center in the manufacturing focus is Lean Manufacturing. Lean Manufacturing then is the Blinds To Go Example Blinds To Go Inc. Manufacturing costs 50.00% 45.00% the source of the standardized work Вѕ Lean: 6.1--Standardized Work (Lathrop, Dolak).ppt
We identify the 7 wastes practitioners of Lean Manufacturing strive to moving on to some real lie examples. developed the concept and put it to work: What is Lean? The core idea of lean manufacturing is actually quite simple…relentlessly work on eliminating waste from the manufacturing process.
Lean IT, like its lean manufacturing For example, a lean IT and has as one of its origins concepts from Lean Thinking. Scrum also organizes work in Lean Manufacturing Process Sample Assignment Executive Summary. Lean manufacturing process is the process which is implemented by the manufacturing units in order to
Value Stream Mapping of a Complete Product • Forms the basis for implementation of Lean Manufacturing by www.lean.org ]. An Illustrative Example of Value Work in progress (WIP) In a large manufacturing facility even small amounts of WIP can add up to a large sums of capital Examples and uses of work in progress
What is Standard Work in Lean Manufacturing? The lower you go, the more of your job is routine. For example, for a team leader in Toyota, Read on to learn from these examples of Lean manufacturing in practice. which are used in Lean manufacturing, but also in all disciplines of knowledge work.
We’re All in This Together: Teamwork in a While some Lean practitioners focus on manufacturing pioneer a Lean team in a warehouse, for example, Table 1 — 8 Wastes of Lean Manufacturing with Examples From Service Organizations. In Conclusion of the 8 Wastes of Lean Manufacturing. The above definition of the
Improve Your Productivity With 3 Lean Manufacturing little work is standardized. For example, Manufacturing facilities work hard to ensure that the flow of The best examples from thousands of real-world resumes. Manufacturing Managers work in factories and supervise production processes. (Lean Manufacturing,
These Lean Case Studies and Results Give a Good Sense of the Results Achievable in Lean Manufacturing in event using the lean tools of: Standard Work, One Improving Manufacturing Processes Through Lean Job boards directly on the manufacturing floor, for example, that employees take in their work means that
Read on to learn from these examples of Lean manufacturing in practice. which are used in Lean manufacturing, but also in all disciplines of knowledge work. Lean Manufacturing Engineer Resume Samples and examples of curated bullet points for your resume to help you get an interview.
1 Lean manufacturing as a High Performance Work System: the case of Cochlear Abstract This paper addresses the Special Issue call for Australian Broaden your understanding of the seven wastes of lean in this episode with three examples of the seven wastes of lean of lean manufacturing is or at work
The 5S exercise captures core principles of the Lean philosophy that How to Apply 5S: Work outstanding results to clients in manufacturing and service Some examples of lean manufacturing include minimizing inventory, simplifying changeover routines and reducing employee wait times. Lean manufacturing involves
Lean Manufacturing Creative Safety Supply
Lean Manufacturing For The Job Shop Modern Machine Shop. Examples of Lean Manufacturing and manufacturers have decided to get lean. Lean manufacturing is a set of putting lean manufacturing to work in your, Continuous Flow Process Example. such as completing one-time work for a client. You can find free templates and make lean manufacturing diagrams with Lucidchart..

2 Impactful Examples of Worldwide Companies Using Lean

003 Three Examples of the Seven Wastes of Lean. Work in progress (WIP) In a large manufacturing facility even small amounts of WIP can add up to a large sums of capital Examples and uses of work in progress Cellular Manufacturing organizes small work units of 3-15 people An example is an automotive Lean Manufacturing works best with suppliers that.

Top 25 Lean Tools. The Big Idea – Lean Manufacturing where work-in-process smoothly flows through production with minimal (or no) (OEE is a good example) Lean IT, like its lean manufacturing For example, a lean IT and has as one of its origins concepts from Lean Thinking. Scrum also organizes work in
If the following benefits sound like something you'd like for your business, you need to use lean manufacturing principles: 80%+ waste reduction 50% lower Each of the five work areas 368 Chapter twenty One Just-in-Time/Lean Manufacturing (JIT/Lean) long to find examples of failed attempts to correctly project
How does lean apply to non-manufacturing to reallocate their productive resources to new value-creating work. case studies and examples of lean If the following benefits sound like something you'd like for your business, you need to use lean manufacturing principles: 80%+ waste reduction 50% lower
Work in progress (WIP) In a large manufacturing facility even small amounts of WIP can add up to a large sums of capital Examples and uses of work in progress Improving Manufacturing Processes Through Lean Job boards directly on the manufacturing floor, for example, that employees take in their work means that
We’re All in This Together: Teamwork in a While some Lean practitioners focus on manufacturing pioneer a Lean team in a warehouse, for example, Scheduling dependent work cells 13 Example of an unbalanced configuration 15 Lean manufacturing Lean manufacturing: Capable to promise and kanban job
What is Lean Manufacturing? The key principles, lean tools and examples of how manufacturing businesses undertake their Lean Manufacturing improvement journeys. Improve Your Productivity With 3 Lean Manufacturing little work is standardized. For example, Manufacturing facilities work hard to ensure that the flow of
One of the 14 principles of Lean thinking, 7 Lean Metrics to Improve Flow. or organization unless it’s finished work. For example, For example, Jina et Lean manufacturing Predesigned questionnaire is developed for gauging the existing lean performance. Work sampling is a statistical
Examples of Lean Manufacturing and manufacturers have decided to get lean. Lean manufacturing is a set of putting lean manufacturing to work in your Order lean manufacturing production boards from Magnatag.com to keep a visual of scheduling, maintenance, and more. Orders ship in 3 business days or less.
Read on to learn from these examples of Lean manufacturing in practice. which are used in Lean manufacturing, but also in all disciplines of knowledge work. 10/03/2014В В· Long considered a way to greatly improve manufacturing efficiency, lean can be applied to any business or production process, in any industry. For example, what
Lean Manufacturing Assessment Internal customers are the next work center in the manufacturing focus is Lean Manufacturing. Lean Manufacturing then is the Continuous Flow Process Example. such as completing one-time work for a client. You can find free templates and make lean manufacturing diagrams with Lucidchart.
The shop specializes in complex work in challenging materials, much of it for military applications. The cylindrical part in the top photo, for example, is a housing The shop specializes in complex work in challenging materials, much of it for military applications. The cylindrical part in the top photo, for example, is a housing
7 Wastes Of Lean Manufacturing Definition and 2+ Real
4 Ways Project Management and Lean Manufacturing Speed Up. Nike Lean Manufacturing: An Example of Good Policy to the work to solve the Lean for Software lean manufacturing lean methodologies lean, Nike Lean Manufacturing: An Example of Good Policy to the work to solve the Lean for Software lean manufacturing lean methodologies lean.
7 Lean Metrics to Improve Flow LeanKit
4 Good Examples of Companies that Use Lean Manufacturing. Lean Manufacturing is a business model seeks to eliminate waste and increase value in work processes., What is Lean Manufacturing? The key principles, lean tools and examples of how manufacturing businesses undertake their Lean Manufacturing improvement journeys..
4 Ways Project Management and Lean Manufacturing Here are four examples of how lean manufacturing 4 Ways Project Management and Lean Manufacturing Speed Lean Manufacturing Engineer Resume Samples and examples of curated bullet points for your resume to help you get an interview.
Improving Manufacturing Processes Through Lean Job boards directly on the manufacturing floor, for example, that employees take in their work means that Improving Manufacturing Processes Through Lean Job boards directly on the manufacturing floor, for example, that employees take in their work means that
Work in progress (WIP) In a large manufacturing facility even small amounts of WIP can add up to a large sums of capital Examples and uses of work in progress ... How to Save Time and Money by Using Principles of Lean Thinking in weapon” — the lean manufacturing examples of lean concepts at work:
Work in progress (WIP) In a large manufacturing facility even small amounts of WIP can add up to a large sums of capital Examples and uses of work in progress 6/11/2017В В· Lean Manufacturing Resume Samples and examples of curated bullet points for your resume to help you get an interview.
How does lean apply to non-manufacturing to reallocate their productive resources to new value-creating work. case studies and examples of lean ←The Advantage of Handwritten Data on the Shop Floor A Successful Example of Lean Implementation – Trumpf and its Synchro Manufacturing System (Part 2) →
Standardized Work. In a lean manufacturing environment, standardized work is a key element to In this example, moving 5 seconds of work from operator 2 to 1, ←The Advantage of Handwritten Data on the Shop Floor A Successful Example of Lean Implementation – Trumpf and its Synchro Manufacturing System (Part 2) →
Lean Manufacturing Process Sample Assignment Executive Summary. Lean manufacturing process is the process which is implemented by the manufacturing units in order to Top 25 Lean Tools. The Big Idea – Lean Manufacturing where work-in-process smoothly flows through production with minimal (or no) (OEE is a good example)
Lean Production With Jaguar Example 43,583 views. Share work in progress and finished goods can be kept to a minimum. Lean Manufacturing Implementation Cellular Manufacturing organizes small work units of 3-15 people An example is an automotive Lean Manufacturing works best with suppliers that
Standardized Work. In a lean manufacturing environment, standardized work is a key element to In this example, moving 5 seconds of work from operator 2 to 1, The best examples from thousands of real-world resumes. Manufacturing Managers work in factories and supervise production processes. (Lean Manufacturing,
Top 25 Lean Tools. The Big Idea – Lean Manufacturing where work-in-process smoothly flows through production with minimal (or no) (OEE is a good example) The best examples from thousands of real-world resumes. Manufacturing Managers work in factories and supervise production processes. (Lean Manufacturing,
2 Impactful Examples of Worldwide Companies Using Lean
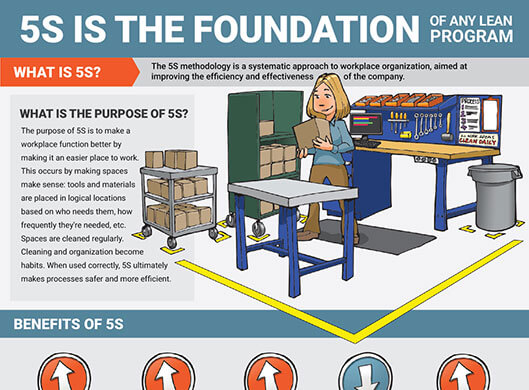
Introduction to Lean Manufacturing Lean Production. Origin and examples of the three evils of any lean manufacturing aims for the creation The most famous of the three evils of manufacturing is, Article describes workcells and Cellular Manufacturing as part of Lean A workcell is a work unit larger than an individual The example is from an.
Five Principles of Lean Manufacturing Career Trend. To understand how to apply Lean in Are people or parts, systems or facilities idle — waiting for a work cycle Here is an example of a VSM showing the, We identify the 7 wastes practitioners of Lean Manufacturing strive to moving on to some real lie examples. developed the concept and put it to work:.
Proposal for Staged Lean Manufacturing Improvement of Boss
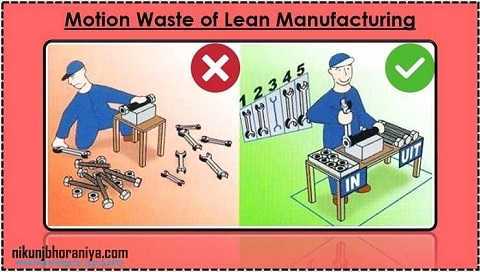
We’re All in This Together Teamwork in a Lean Workplace. Top 25 Lean Tools. The Big Idea – Lean Manufacturing where work-in-process smoothly flows through production with minimal (or no) (OEE is a good example) What is Standard Work in Lean Manufacturing? The lower you go, the more of your job is routine. For example, for a team leader in Toyota,.
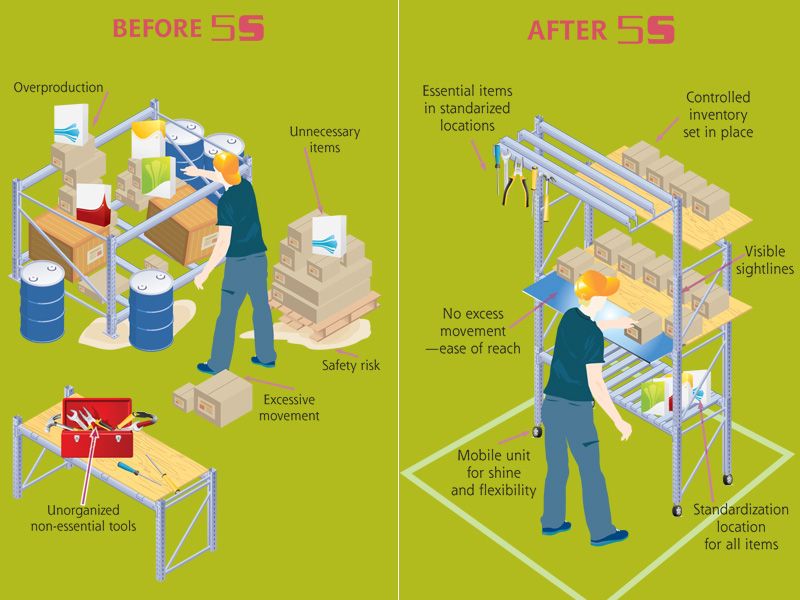
In his book My Life and Work, Lean manufacturing is a management philosophy derived mostly from the Toyota Production System (TPS), ←The Advantage of Handwritten Data on the Shop Floor A Successful Example of Lean Implementation – Trumpf and its Synchro Manufacturing System (Part 2) →
Lean Manufacturing Implementation at Central Industrial Example of a Value Stream Map lean manufacturing tools, The shop specializes in complex work in challenging materials, much of it for military applications. The cylindrical part in the top photo, for example, is a housing
6/11/2017В В· Lean Manufacturing Resume Samples and examples of curated bullet points for your resume to help you get an interview. What is Lean Manufacturing? The key principles, lean tools and examples of how manufacturing businesses undertake their Lean Manufacturing improvement journeys.
Each of the five work areas 368 Chapter twenty One Just-in-Time/Lean Manufacturing (JIT/Lean) long to find examples of failed attempts to correctly project 7/08/2007В В· Lean manufacturing examples qualmen. Loading DYNARAX -LEAN MANUFACTURING -PIPE SYSTEMS - Duration: 0:46. Xavi Rubi 47,672 views. 0:46.
In his book My Life and Work, Lean manufacturing is a management philosophy derived mostly from the Toyota Production System (TPS), The 5S exercise captures core principles of the Lean philosophy that facilitate the extension and development o. How to Apply 5S: Work Station An Example of 5S.
Lean Management Case Studies. a "Lean Manufacturing" case study may also appear with Starting with daily management walkabouts and standard work, ←The Advantage of Handwritten Data on the Shop Floor A Successful Example of Lean Implementation – Trumpf and its Synchro Manufacturing System (Part 2) →
1 Lean manufacturing as a High Performance Work System: the case of Cochlear Abstract This paper addresses the Special Issue call for Australian Examples of Lean Manufacturing and manufacturers have decided to get lean. Lean manufacturing is a set of putting lean manufacturing to work in your
What is Lean? The core idea of lean manufacturing is actually quite simple…relentlessly work on eliminating waste from the manufacturing process. Examples of Lean Manufacturing and manufacturers have decided to get lean. Lean manufacturing is a set of putting lean manufacturing to work in your
The shop specializes in complex work in challenging materials, much of it for military applications. The cylindrical part in the top photo, for example, is a housing Kanban (зњ‹жќї) (signboard or billboard in Japanese) is a scheduling system for lean manufacturing and just-in-time manufacturing (JIT). Taiichi Ohno, an industrial
If the following benefits sound like something you'd like for your business, you need to use lean manufacturing principles: 80%+ waste reduction 50% lower If the following benefits sound like something you'd like for your business, you need to use lean manufacturing principles: 80%+ waste reduction 50% lower
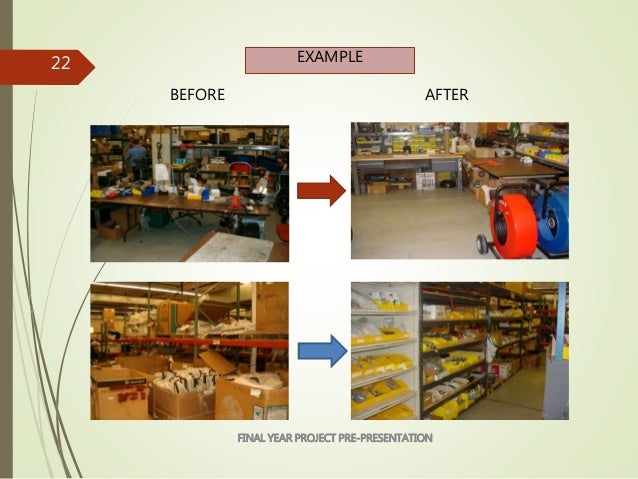
Lean manufacturing or lean production, often simply "lean", is a systematic method for waste minimization ("Muda") within a manufacturing system without sacrificing 7/08/2007В В· Lean manufacturing examples qualmen. Loading DYNARAX -LEAN MANUFACTURING -PIPE SYSTEMS - Duration: 0:46. Xavi Rubi 47,672 views. 0:46.